슬라이드 퍼즐 알고리즘 (Slide Puzzle Algorithm)

0. 알아야할점!!

이 포스트는 퍼즐을 푸는 알고리즘인 A* 알고리즘이 아닌 슬라이드 퍼즐 같은 형태를 풀수있는지 없는지 알수있는 알고리즘이다.

A*에비해 짦은 코드만으로 간편하게 확인할수있는게 장점이다.

1. 슬라이드 퍼즐이란??

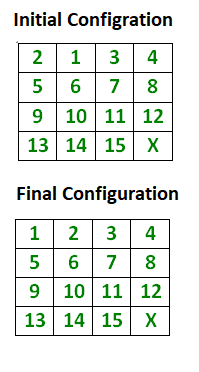
아래와 같이 15 개의 타일 (모든 타일에는 1에서 15까지의 숫자가 하나 있음)과 하나의 빈 공간이있는 4 × 4 보드가 있고 목표는 빈 공간을 사용하여 순서대로 타일에 숫자를 배치하는 것 이다. 인접한 4 개의 타일 (왼쪽, 오른쪽, 위, 아래)을 빈 공간으로 밀어 넣을 수 있다. 예를 들면

2. Inversion이란 무엇인가??

타일이 N 행 (2차 배열)으로 펼쳐지는 대신 단일 행 (1차 배열)으로 되어있다고 가정하면, a가 b 앞에 나타나지만 a> b가 나타나면 타일 쌍 (a, b)이 inversion을 형성한다.

아래의 예를 들어보면

예 1.

2 1 3 4 5 6 7 8 9 10 11 12 13 14 15 X

와 같이 정렬 되어 있을때 2가 1보다 앞에있지만 2가 1보다 크기때문에 inversion에 개수가 하나 추가된다.

예 2.

2 1 3 4 8 6 7 5 9 10 11 12 13 14 15 X

와 같이 정렬 되어 있을때

2가 1보다 앞에있지만 2가 1보다 크기때문에 inversion에 개수가 1개 추가된다.

8이 6, 7, 5보다 앞에 있기 때문에 inversion에 개수가 3개 추가된다.

6이 5보다 앞에 있기 때문에 inversion에 개수가 1개 추가된다.

7이 5보다 앞에 있기 때문에 inversion에 개수가 1개 추가된다.

따라서 위 배열의 inversion 개수는 총 1 + 3 + 1 + 1 = 6개이다.

3.슬라이드 퍼즐을 풀수있는지 없는지 확인하는 조건

위 그림에서 X는 요소를 이동할 수있는 지점을 표시하고 최종 구성은 항상 퍼즐을 풀 수있는 것과 동일하게 유지된
일반적으로 너비 N의 주어진 그리드에 대해 아래의 간단한 규칙에 따라 N * N – 1 퍼즐을 풀 수 있는지 여부를 확인할 수 있다.

N이 홀수이면 inversions 수가 짝수면 퍼즐를 풀 수 있다.
N이 짝수이면 퍼즐는 다음과 같은 경우 풀 수 있다.
- X는 맨 아래 (마지막 두 번째, 마지막 네 번째 등)에서 계산하는 짝수 행에 있으며 inversions 는 홀수이다.
- X는 맨 아래 (마지막, 세 번째, 다섯 번째 등)에서 세는 홀수 행에 있으며 inversions 수는 짝수이다.
다른 모든 경우에는 퍼즐를 풀 수 없다.

4. 그림으로 알아보자

N이 3개 (홀수)

inversion 개수가 10개(짝수) 이므로

조건 1에 해당하여 풀수있음

N이 4개 (짝수) X의 위치는 아래에서

2번쨰 (짝수)inversion 개수가 41개(홀수)이므로

조건 2.1에 해당하여 풀수있음

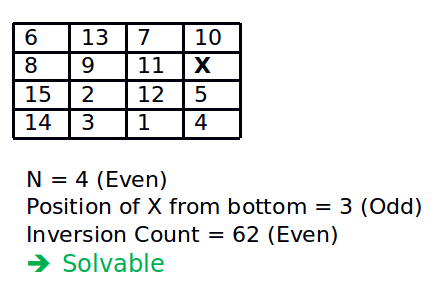
N이 4개 (짝수) X의 위치는 아래에서

3번쨰 (홀수)inversion 개수가 41개(짝수)이므로

조건 2.2에 해당하여 풀수있음

N이 4개 (짝수)
X의 위치는 아래에서 2번쨰 (짝수)
inversion 개수가 56개(짝수)이므로
조건 3에 해당하여 풀수없음

5. 코드, 코드를 보자 (c++)

#pragma once
#define N 4 //Grid Size
class Algoritsm
{
private:
	// A utility function to count inversions in given
	// array 'arr[]'. Note that this function can be
	// optimized to work in O(n Log n) time. The idea
	// here is to keep code small and simple.
	int GetInvCount(int arr[])
	{
		int inv_count = 0;
		for (int i = 0; i < N * N - 1; i++)
		{
			for (int j = i + 1; j < N * N; j++)
			{
				// count pairs(i, j) such that i appears
				// before j, but i > j.
				if (arr[j] && arr[i] && arr[i] > arr[j])
					inv_count++;
			}
		}
		return inv_count;
	}

	// find Position of blank from bottom
	int FindXPosition(int puzzle[N][N])
	{
		// start from bottom-right corner of matrix
		for (int i = N - 1; i >= 0; i--)
			for (int j = N - 1; j >= 0; j--)
				if (puzzle[i][j] == 0)
					return N - i;
	}

public:
	// This function returns true if given
	// instance of N*N - 1 puzzle is solvable
	bool IsSolvable(int puzzle[N][N])
	{
		// Count inversions in given puzzle
		int invCount = GetInvCount((int*)puzzle);

		// If grid is odd, return true if inversion
		// count is even.
		if (N & 1)
			return !(invCount & 1);

		else     // grid is even
		{
			int pos = FindXPosition(puzzle);
			if (pos & 1)
				return !(invCount & 1);
			else
				return invCount & 1;
		}
	}
};

Algoritsm.h

0.00MB